Peer-to-peer networks are composed of multiple nodes that interact with each other, enabling a decentralized system of communication and data exchange. The effective discovery and lookup of nodes are crucial elements that facilitate seamless interaction within this network. Traditionally, the discoverability problem could be addressed by maintaining a central directory, where nodes register themselves and query to find peers’ addresses. However, this method, while solving the discoverability issue, introduces a central point of failure and deviates from the decentralized ethos by requiring the directory to be accessible at all times.
A Brief overview about Kademlia
A more decentralized and resilient solution is provided by the implementation of Kademlia, a distributed hash table (DHT) utilized in numerous decentralized protocols, including BitTorrent, Ethereum, and IPFS. DHTs are adept at storing information about the locations of nodes and the data they hold, significantly enhancing search and discovery processes within the network.
In Kademlia, nodes are placed in a one-dimensional space and assigned unique IDs. The architecture employs a novel metric known as ‘distance’ to ascertain the proximity between nodes, calculated through the XOR operation on their IDs. This choice of metric offers several benefits: The distance between a node and itself is always zero, ensuring reflexivity; it adheres to symmetry, meaning the distance from node A to B is identical to the distance from B to A; and it satisfies the triangle inequality principle, whereby the direct distance between two nodes is always less than the sum of distances through an intermediary node.
To further refine the efficiency of node discovery and data retrieval, Kademlia integrates two key components: k-buckets and routing tables. K-buckets are data structures used within each node to store information about other nodes. Each k-bucket corresponds to a specific range of distances and holds a limited number of node contacts, prioritizing those that have been seen recently. This ensures that the network can adapt to changes and maintain up-to-date information on active nodes.
Routing tables, on the other hand, aggregate these k-buckets and form the backbone of the node discovery mechanism in Kademlia. They enable a node to determine the best candidates for routing a query based on the desired key or node ID, leveraging the XOR metric for distance. By dividing the network into smaller, manageable segments, routing tables facilitate efficient pathfinding and data lookup operations, ensuring that queries can be resolved by traversing the network in logarithmic steps relative to its size.
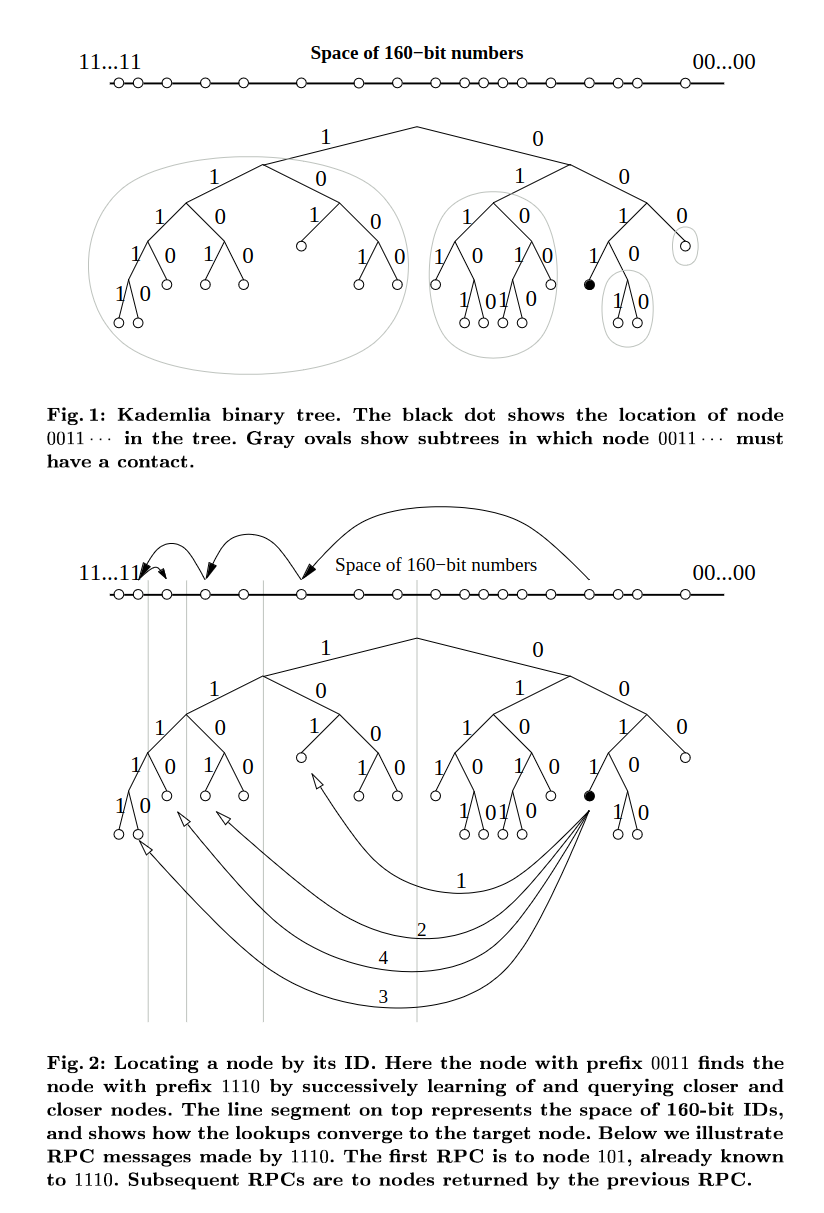
Image Source: Maymounkov, et al.
Read more about kademlia here.
Multidimentional distributed hash table
Traditional DHTs like Kademlia operate on a simple principle: each node and data piece is assigned a unique identifier (ID), and the “distance” between these IDs determines their relationship and routing logic. While effective in linear, one-dimensional keyspaces, this model struggles with the complexity of multidimensional data, where the relationship between data points cannot be adequately captured by a single metric.
The proposed solution introduces a multidimensional extension to Kademlia by adopting a bitwise approach to both node placement and distance calculation.
Bit Representation of Coordinates
Consider a node with coordinates in a 2D space, represented as (X,Y). Each coordinate is broken down into a binary representation: X as [x1,x2,x3,…] and Y as [y1,y2,y3,…]. This binary breakdown allows us to treat the multidimensional space as a series of binary decisions (left/right, up/down), simplifying the routing logic.
Iterative Space Partitioning and Searching
Starting with the entire 2D plane, we define an initial search rectangle using the most significant bits (MSBs) of the target’s coordinates, T(X,Y). This rectangle is then iteratively subdivided, using the next set of bits to progressively narrow down the search area. This process continues until we’ve isolated a sufficiently small region likely to contain the target node.
Example:
Let’s say we’re searching for a target node T with coordinates represented by the bits X=101,Y=010. Our initial rectangle is defined by the MSBs of X and Y, isolating one quadrant of the 2D plane. With each iteration, we use the next bit to halve the search area, quickly zeroing in on the target’s location.
Searching in this case would look like this:
| Iteration |
X coordinate |
Y coordinate |
| 1 |
100<=X<=111 |
000<=Y<=011 |
| 2 |
100<=X<=101 |
010<=Y<=011 |
| 3 |
101<=X<=101 |
010<=Y<=010 |
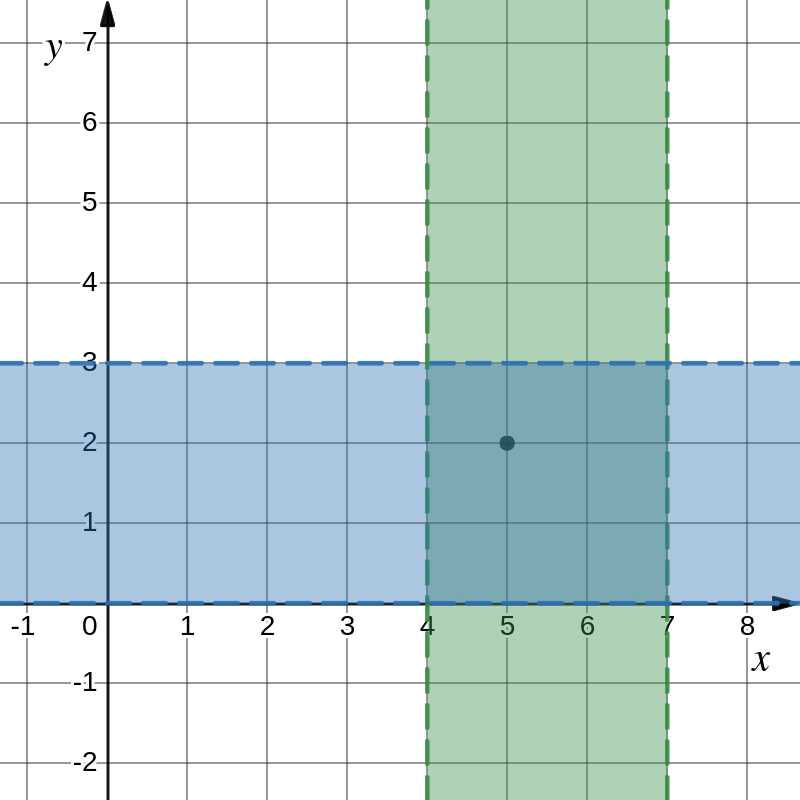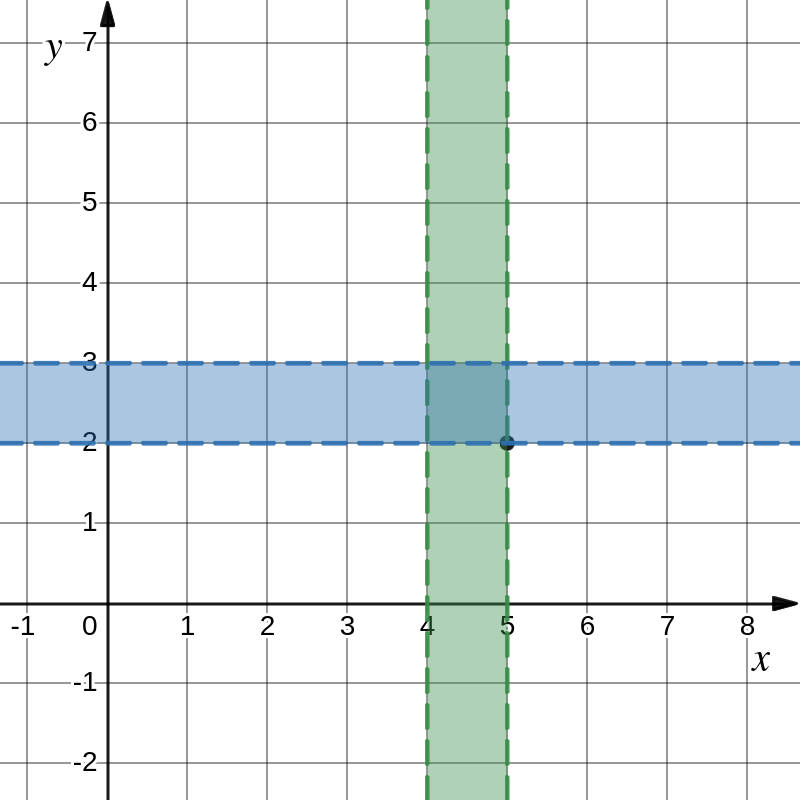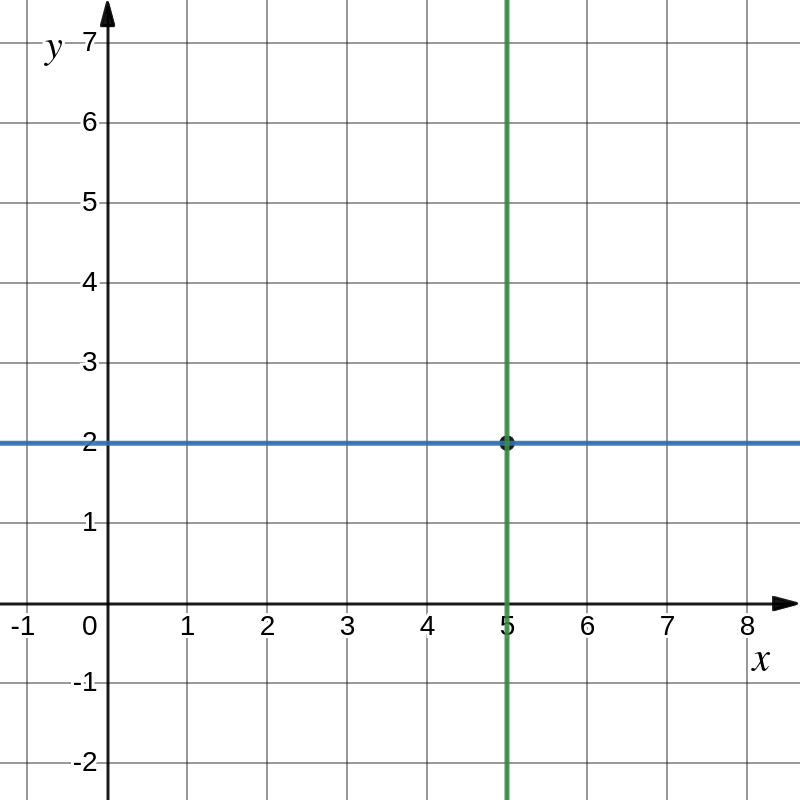
Image: searching for a node in multidimensional DHT
Routing Table Design
In this system, the routing table must accommodate the multidimensional nature of the data. Each entry in the table corresponds to a specific combination of bits, representing a distinct “region” of the multidimensional space. Nodes within the same region share similar bit prefixes, allowing for efficient grouping and lookups.
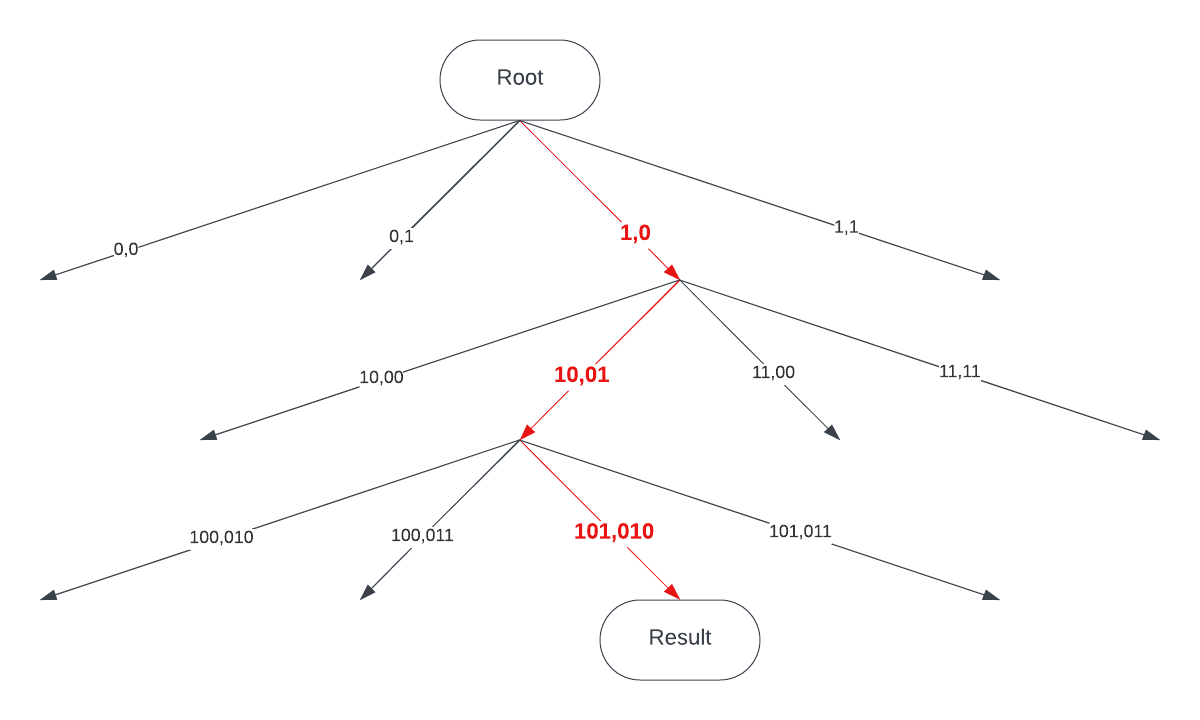
Image: Routing table search for a node with ‘distance’ of X=101,Y=010
Dynamic dimension changing nodes
Another approach that can help in reducing the number of hops in the multidimensional distributed hash table (DHT) system as compared to Kademlia is the concept of dynamically dimension changing nodes. This allows nodes to adjust their position within the multidimensional space based on various factors, such as network demand, data distribution, or even to optimize routing efficiency.
Example:
A node in 2D that is being accessed frequently from the entire topography can be moved and made 3D, making it closer to a lot of nodes in the ecosystem, and this can continue until n dimentions.
Note: A system potentially needs to fix the maximum number of dimentions the network can handle beyond which is a tipping point, and computation takes up more time than hopping ever would. Also, dimensional hopping would introduce certain factors to consider, such as the consensus mechanism for node value in space.
In the case of a new, non-existing dimension, the routing table can add on another pointer from the parent node to signify a new dimension of search.
Note: The material presented on this website reflects my personal views and expressions. Please ensure proper attribution is given when using or referencing this content.